Integer Pairs Between Two Circles

Problem Link

This coding practice problem is copyrighted by Grepp Co., Ltd.

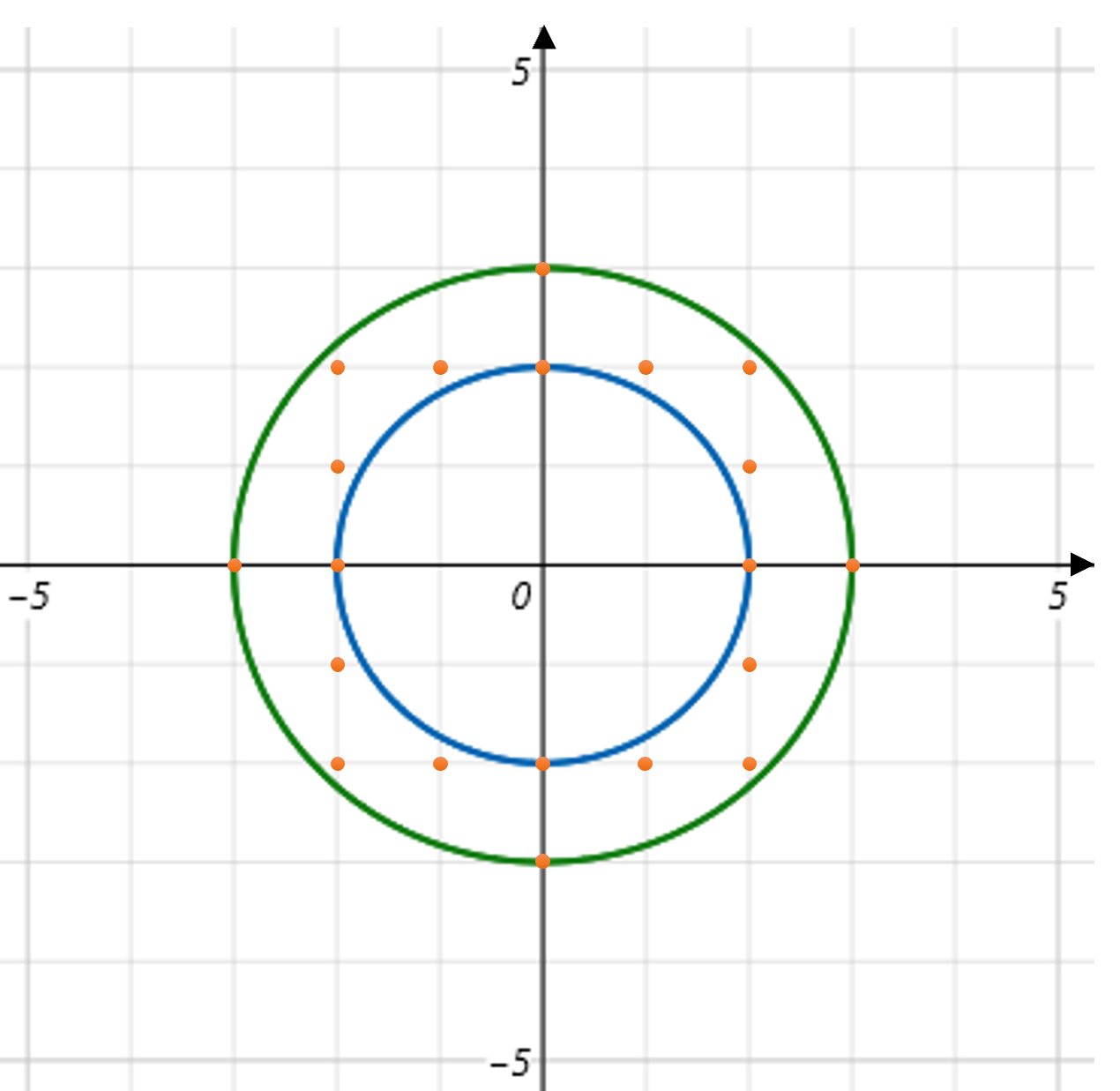
In a 2D Cartesian coordinate system with the origin at the center, two circles of different sizes are given. When two integers r1 and r2 representing the radii are provided as parameters, complete the solution functions to return the number of points with both x and y coordinates as integers that lie in the space between the two circles.

※ Points on the circles are also included in the count

Constraints

$1 \le r1 \le r2 \le 1,000,000$

I/O Example

r1	r2	result
2	3	20

As shown in the illustration, there are a total of 20 points with integer pairs.

C++

#include <cmath>
#include <iostream>
using namespace std;

long long solution(int r1, int r2) {
    // Initialize the answer to count points on the y-axis that lie between r1 and r2
    // This includes points within and on the boundary of the two circles along the y-axis.
    long long result = r2 - r1 + 1;
    
    long long rr1 = static_cast<long long>(r1) * r1;
    long long rr2 = static_cast<long long>(r2) * r2;

    // Loop through each x-coordinate from 1 to r2 (not including 0 as it's already counted)
    for (int x = 1; x < r2; x++) { 
        long long xx = static_cast<long long>(x) * x;
        int maxY = static_cast<int>(sqrt(rr2 - xx));

        if (x < r1) { // If x is within the smaller circle
            int minY = static_cast<int>(ceil(sqrt(rr1 - xx)));
            result += maxY - minY + 1;
        } else result += maxY; // If x is outside the smaller circle
    }
    return result * 4;
}