Container With Most Water

Problem Link

You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the iᵗʰ line are (i, 0) and (i, height[i]).

Find two lines that together with the x-axis form a container, such that the container contains the most water.

Return the maximum amount of water a container can store.

Notice that you may not slant the container.

Example 1:

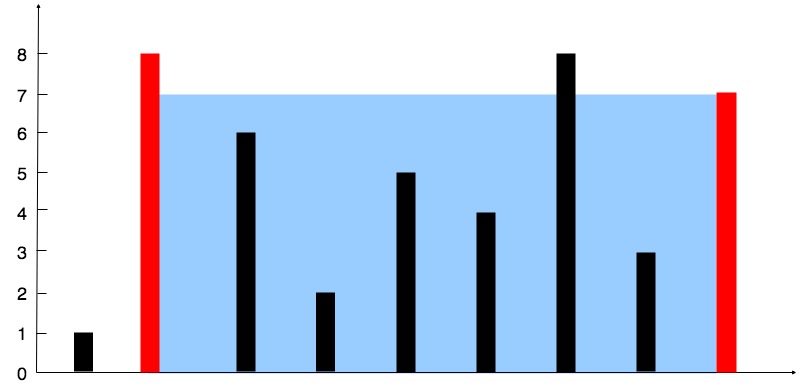
• Input: height = [1, 8, 6, 2, 5, 4, 8, 3, 7]
• Output: 49
• Explanation: The above vertical lines are represented by array [1, 8, 6, 2, 5, 4, 8, 3, 7]. In this case, the max area of water (blue section) the container can contain is 49.

Example 2:

• Input: height = [1, 1]
• Output: 1

Constrains:

• n == height.length
• 2 <= n <= 10⁵
• 0 <= height[i] <= 10⁴

class Solution {
public:
    int maxArea(vector<int>& height) {
        int max_area = 0; // Initialize variable to store the maximum area
        int left = 0; // Start pointer
        int right = height.size() - 1; // End pointer
        
        while (left < right) { // Repeat while the start pointer is less than the end pointer
            // Calculate the area with the distance between pointers and the lower height
            int current_area = (right - left) * min(height[left], height[right]);
            max_area = max(max_area, current_area); // Update maximum area
            
            // Move the pointer with the lower height
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }
        
        return max_area; // Return the calculated maximum area
    }
};